Soft tissue is composed of closely packed groups of cells entrapped in a network of fibers through which water percolates. At a microscopic scale, the tissue components have no pronounced boundaries. They appear to merge into a continuous structure with spatial variations in the refractive index. It has been shown that the tissue components that contribute most to the local refractive-index variations are the connective tissue fibers (bundles of elastin and collagen), cytoplasmic organelles (mitochondria, lysosoms, and peroxisomes), cell nuclei, and melanin granules [1]. For different parts of a biological cell, values of refractive index in the NIR range can be estimated as follows: extracellular fluid, n = 1.351.36; cytoplasm, 1.360-1.375, cell membrane, 1.46, nucleus, 1.38-1.41; mitochondria and organelles, 1.38-1.41; melanin, 1.6-1.7.
Scattering arises from mismatches in refractive index of the components that make up the cell. Organelles and subcomponents of organelles having indices different from their surroundings are expected to be the primary sources of cellular scattering. For instance, the nucleus is a significant scatterer because it is often the largest organelle in the cell, and its size increases relative to the rest of the cell throughout neoplastic progression. Mitochondria (0.5-1.5 pm in diameter), lysosomes (0.5 pm), and peroxisomes (0.5 pm) are very important scatterers whose size relative to the wavelength of light suggests that they must make a significant contribution to backscattering. Granular melanin, traditionally thought
|
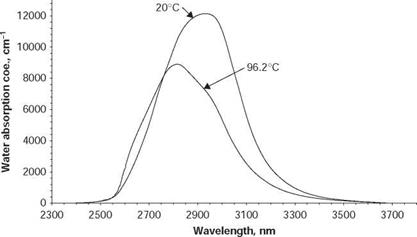
Figure 3.7 Shifting of water absorption spectrum at temperature increase [13]. |
of as an absorber, must be considered an important scatterer because of its size and high refractive index. Besides cell components, fibrous tissue structures such as collagen and elastin must be considered important scatterers.
The refractive indices of tissue structure elements, such as the fibrils, the interstitial medium, nuclei, cytoplasm, organelles, and the tissue itself can be derived using the law of Gladstone and Dale, which states that the resulting value represents an average of the refractive indices of the components related to their volume fractions as [1]:
N
n = X, X f = 1, (3.3)
i =1 і
where nl and f are the refractive index and volume fraction of the individual components, respectively, and N is the number of components.
The average background index is defined as the weighted average of refractive indices of the cytoplasm and the interstitial fluid, ncp and nis, as
П0 = fcpncp + (1 – -0^ (3.4)
where f is the volume fraction of the fluid in the tissue contained inside the cells. Litera-
cp
ture data presented allows one to estimate ncp = 1.367 and nis = 1.355. Since approximately 60% of the total fluid in soft tissue is contained in the intracellular compartment, it follows from Eq. (3.4) that n0 = 0.6-(1.367) + 0.4-(1.355) = 1.362. The refractive index of scatterers can be defined as the sum of the background index and the mean index variation, n = n0 + <An>, which can be approximated by another volume-weight average,
<An> = ff(nf – nis) + fnc(nnc – ncp) + for(nor – ncp). (3.5)
Here the subscripts f, is, nc, cp, and or refer to the fibers, interstitial fluid, nuclei, cytoplasm, and organelles, respectively, which were identified above as the major contributors to index variations. The terms in parentheses in this expression are the differences between the refractive indices of the three types of tissue component and their respective backgrounds; the multiplying factors are the volume fractions of the elements in the solid portion of the tissue. The refractive index of the connective-tissue fibers is about 1.47, which corresponds to about 55% hydration of collagen, its main component. The nucleus and the cytoplasmic organelles in mammalian cells that contain similar concentrations of proteins and nucleic acids, such as mitochondria and the ribosomes, have refractive indices that lie within a relative narrow range (1.38-1.41). Taking this into account and assuming that nnc = nor = 1.40, the mean index variation can be expressed in terms of the fibrous-tissue fraction cf only: <An> = f(nf – nis) + (1 – f) (nnc – ncp).
Collagen and elastin fibers compose approximately 70% of the fat-free dry weight of the dermis. Therefore, for dermis f = 0.7, nf – nis = 1.470-1.355 = 0.115 and nnc – ncp = nor – ncp = 1.400-1.367 = 0.033, the mean index variations <An> = 0.7 • (0.115) + (1-0.7)-(0.033) = 0.09 and П = n0 + <An> ~ 1.36 + 0.09 = 1.45. The mean refractive index of skin or any other tissue can be evaluated using the law of Gladstone and Dale with respect to a two-phase system: scatterers with volume fraction of fs and background material with volume fraction (1 – fs)
In practice, the mean refractive index of a tissue is a measurable value, thus volume fraction of scatterers could be determined from Eq. (3.6). For example, for skin dermis RI measured in vivo on the wavelength of He-Ne laser (633 nm) n = 1.396 [1]; thus, using the estimates presented above for ns = 1.45 and n0 = 1.36, we can determine the volume fraction of scatterers as f ~ 0.4. This parameter is very important for evaluation and monitoring of skin scattering, that is, skin appearance, especially at its aging or influence of bad ecology or in a course of its rejuvenation. Scatterer volume fraction determination is also important for evaluation of efficiency of skin sun (UV) protective screens based on scattering particles.