3.1.3 Light Absorption and Scattering
Absorbing medium is the medium that absorbs light at certain wavelengths or wavelength bands. The absorption band is a range of wavelengths for which a medium absorbs more strongly than at adjacent wavelengths. The process of light absorption is the transformation of light (radiant) energy to some other form of energy, usually heat, as the light transverses tissue. Commonly, an absorbing medium consists of absorption centers that are particles or molecules that absorb light. To characterize the absorption of a medium, an absorption coefficient pa is introduced; in a nonscattering sample it is defined as the reciprocal of the distance xa over which light of intensity I(x = 0) = I0 is attenuated (due to absorption) to I(xa) = I0/e~ 0.37I0; the units are typically cm-1 or mm-1. Behind this definition is a fundamental process of light wave or photon absorption that is characterized by a cross section, that is, the ability of a molecule to absorb a photon of a particular wavelength and polarization. Although the units are given as an area, it does not refer to an actual area size, at least partially because the density or state of the target molecule will affect the probability of absorption. Quantitatively, the number dN of photons absorbed between the points x and x + dx along the path of a light beam is the product of the number N of photons penetrating to depth x times the number p of absorbing molecules per unit volume times the absorption cross section sabs: dN/dx = – psabsN, pa = psabs.
In spectroscopy, a few terms are commonly used, such as absorbance that is the ratio of the absorbed light intensity to the incident intensity, thus, it is a dimensionless quantity and absorption spectrum, that is, the spectrum formed by light that has passed through a medium in which light of certain wavelengths was absorbed.
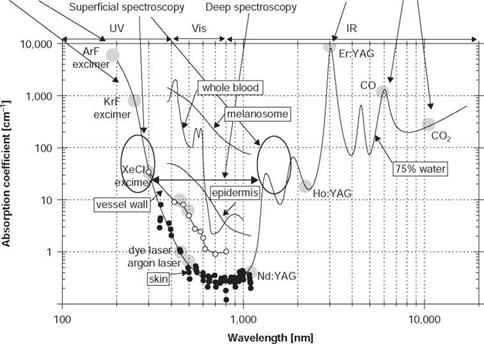
Absorption spectra can be also expressed in terms of absorption coefficient. Such spectra for skin and its components: water (75%), epidermis, melanosome, vessel wall, and whole blood are presented in Fig. 3.2 . The diagnostic/therapeutic lasers and their wavelengths are presented on the crossings of water absorption curve, and the corresponding laser
|
Diagnostic/therapeutic window Superficial treatment Superficial treatment
Figure 3.2 Absorption spectra of skin and skin components: water (75%), epidermis, melanosome, vessel wall, and whole blood; diagnostic/therapeutic lasers and their wavelengths as well as diagnostic/therapeutic window and wavelength ranges suitable for superficial and deep spectroscopy or treatment are also shown (adapted from ref. [1]). |
wavelengths show what absorption coefficient is expected at absorption in water. Because water is the major component of any tissue, including skin, presented absorption coefficients will be only slightly corrected for real tissues. As seen in Fig. 3.2, for bloodless skin in the visible range, absorption is equal to water (75%), because dermis as the main skin component that is well supplied by water defines the absorption coefficient in this range.
In photomedicine, many diagnostic and treatment technologies use endogenous or exogenous agents—photosensitizers that are substances that increase the absorption of a tissue at a particular wavelength band, and may significantly accelerate photothermal or photochemical treatments.
Tissues are not only absorbing, but also an inhomogeneous media with different levels of organization that include cells, fibers, and macroinhomogeneities, such as, for instance, skin appendages or tumors. The sizes of cells and tissue structure elements vary in size from a few tenths nanometers to hundreds of micrometers [1]. Mammalian cells have diameters in the range of 5-75 pm. In the epidermal layer, the cells are large (with an average cross-sectional area of about 80 pm2 for living epidermis and 1300 pm2 for the outmost horny layer) and quite uniform in size. Fat cells, each containing a single lipid droplet that nearly fills the entire cell and therefore results in eccentric placement of the cytoplasm and nucleus, have a wide range of diameters from a few microns to 50-75 pm. Fat cells may reach a diameter of 100-200 цш in pathological cases. There are a wide variety of structures within cells that determine tissue light scattering. Cell nuclei are on the order of 5-10 цш in diameter; mitochondria, lysosomes and peroxisoms have dimensions of 1-2 цш; ribosomes are on the order of 20 nm in diameter; and structures within various organelles can have dimensions up to a few hundred nanometers.
In the course of transport (travel) in an inhomogeneous medium with absorption a photon changes its direction due to reflection, refraction, diffraction, or scattering and can be absorbed by an appropriate molecule on its way. Light scattering means a change in the direction of propagation of light in a turbid medium caused by reflection and refraction by microscopic internal structures. Such small structures that are smaller or comparable with the wavelength of propagating light are commonly called scatterers. A scatterer is an inhomogeneity or a particle of a medium that refracts or diffracts light; light is diffused or deflected as a result of collisions between the wave and particles of the medium.
There are a number of parameters that describe the scattering process. Scattering angle is related to photon scattered by a particle, so that its trajectory is deflected by a deflection (scattering) angle в in the scattering plane and/or by azimuthal angle of scattering j in the plane perpendicular to the scattering plane. Scattering plane is a plane defined by positions of a light source, a scattering particle, and a detector.
To characterize the scattering efficiency of a medium, a scattering coefficient ps is introduced; in a nonabsorbing sample it is defined as the reciprocal of the distance xs over which the light of intensity I(x = 0) = I0 is attenuated (due to scattering) to I(x) = I0/e~ 0.37/0; the units are typically cm-1 or mm-1. Behind this definition is also a fundamental process of photon scattering that is characterized by a photon scattering cross section, that is, the ability of a particle to scatter a photon of a particular wavelength and polarization; although the units are given as an area, it does not refer to an actual size area; quantitatively, the number dN of photons scattered between the points x and x + dx along the path of a light beam is the product of the number N of photons penetrating to depth x times the number p of scattering particles per unit volume times the scattering cross section CTsca: dN7dx = – psscaN. The scattering coefficient fjs (cm-1) describes a medium containing many scattering particles at a concentration described as a volume density p (cm3); the scattering coefficient is essentially the cross-sectional area ssca (cm-1) per unit volume of medium: ps = pssca.
A collimated (laser) beam is attenuated in a thin tissue layer of thickness x in accordance with the exponential law, Bouguer—Beer—Lambert law,
I(x) =/0exp(-mtx>, (3.1)
where I(x) is the intensity of transmitted light measured using a distant photodetector with a small aperture (on-line or collimated transmittance), W/cm2; I0 is the incident light intensity, W/cm2;
mt = ma+ m (3.2)
is the extinction coefficient (interaction or total attenuation coefficient). Therefore, attenuation is a decrease in energy per unit area of a wave or beam of light: it occurs as the distance from the source increases and is caused by absorption or scattering, or both. The attenuation (extinction) coefficient is the reciprocal of the distance over which light of intensity I0 is attenuated to I0/e~ 0.37/0; the units are typically cm-1. The greatest extinction of the forward scattered light is due to particles with dimensions between 1 and 101. The particles with diameters between 1/4 and 1/2 are the dominant backscatterers.
Besides scattering coefficient, scattering process is also characterized by a so-called scattering phase function—the function that describes the scattering properties of the medium, and is in fact the probability density function for a photon traveling in some direction to be scattered in some new direction [1,3]. It characterizes an elementary scattering act: if scattering is relatively symmetric to the direction of the incident wave, then the phase function depends only on the scattering angle в (angle between two directions, the new and former one), р(в). Scattering anisotropy factor, g, is a major parameter of р(в) and is a measure of the amount of forward direction retained after a single scattering event. If a photon is scattered by a particle so that its trajectory is deflected by a scattering angle в, then the component of the new trajectory which is aligned in the forward direction is presented as cose. There is an average scattering angle and the mean value of (cose) is defined as the anisotropy factor g = (cose). The value of g varies in the range from -1 to 1: g = 0 corresponds to isotropic (Rayleigh) scattering, g = 1 to total forward scattering (Mie scattering at large particles), and -1 to total backward scattering.
Rayleigh scattering relates to scattering by small particles (with respect to the wavelength of the incident light) when the scattered irradiance is inversely proportional to 14 and increases as a6 (a is the radius of a particle), and the angular distribution of the scattered light is isotropic. Mie scattering relates to scattering by comparatively large spherical particles, which are of the order of the wavelength, and based on an exact solution of Maxwell’s electromagnetic field equations for a homogeneous sphere. Typical tissues contain both types of scatterers small and large (for instance, cell components and collagen fibers of connective tissues).
Often, such characteristic of turbid materials and tissues as albedo can be useful for the prediction of light propagation in a tissue. Albedo is the ratio of the scattering to extinction cross section (or coefficient); ranges from zero for a completely absorbing medium to unity for a completely scattering medium.
All the above-mentioned issues are related to a single scattering—the scattering process that occurs when a wave undertakes no more than one collision with the particles of the medium in which it propagates. In contrast, in many tissues we have multiple scattering—a scattering process in which, on average, each photon undertakes many scattering events. However, for some tissues or tissue thin slices, single scattering approximation which assumes that the tissue is sufficiently thin for single scattering, accurately estimates the reflection and transmission for the slab and may be valid.
To evaluate what kind of scattering regime is realized, a so-called mean free path length (MFP) may be estimated. MFP is the mean distance between two successive interactions with scattering or absorption which a photon traveling in a scattering-absorption medium is experiencing, MFP = 1/gt. Thus, one can differentiate optically thin (transparent) or optically thick sample that is under investigation. Optical thickness is the depth of a material or medium in which the intensity of light of a given wavelength is reduced by a factor of 1/e (e = 2.7) because of absorption and/or scattering [see Eq. (3.1)]. A sample with high thickness and/or high turbidity that correspond to a few optical thickness depths is optically thick, as well as a sample with a low thickness and/or low turbidity that correspond to one or less than one optical thickness depth is optically thin.
The radiation transfer theory (RTT) is the basic theory allowing one to calculate light distributions in the multiple scattering media with absorption, such as tissues. The heart of this theory is the radiation transfer equation (RTE)-the Boltzmann or linear transport equation, which is a balance equation describing the flow of particles (e. g., photons) in a given volume element that takes into account their velocity c, location г, and changes due to collisions (i. e., scattering and absorption). The basic parameter for this theory is the reduced scattering coefficient that is a lumped property incorporating the scattering coefficient gs and the scattering anisotropy factor g. /j’ = gs(1 – g) (cm-1); gs’ describes the diffusion of photons in a random walk of step size of 1/gs’ (cm), where each step involves isotropic scattering; this is equivalent to description of photon movement using many small steps 1/gs that each involve only a partial (anisotropic) deflection angle if there are many scattering events before an absorption event, that is, ga << g’ (diffusion regime); g’ is useful in the diffusion regime which is commonly encountered when treating how visible and near-infrared light propagates through tissues [1,3].
The transport mean free path (TMFP) of a photon (cm) is defined as lt = (1/g) = (ga + gs)-1, where g’= ga + g’ is the transport coefficient. The TMFP in a medium with anisotropic single scattering significantly exceeds the MFP, к >> V The lt is the distance over which the photon loses its initial direction.
A power law for dependence of the scattering coefficient on the wavelength is typical for many tissues: gs ^ 1-h [1]. For instance, for different tissue structures, associated with skin aging or rejuvenation, parameter h ranges from 1 to 2. The reduced scattering coefficient also obeys a power law, gk 1-h, that was experimentally demonstrated for normal and dehydrated rat skin in an in vitro study for the wavelength range of 500-1200 nm [4]. Parameter h was equal to 1.12 for normal skin and was decreased at topical application of glycerol (mostly dehydration effect): h = 1.09 for 5 min in glycerol, 0.85 for 10 min, 0.52 for 20 min, and 0.9 for the rehydrated sample.
In vivo backscattering measurements for human skin have also demonstrated the power law for the reduced scattering coefficient [5]: g’s = q1-h (cm-1, l in pm). In particular, for reflectance spectra from the human forearm in the wavelength range 700-900 nm, constants q and h were determined as 5.50 ± 0.11 and 1.11 ± 0.08, respectively. From Mie theory, it follows that the power constant h is related to an averaged size of the scatterers with the Mie-equivalent radius aM. Once h is determined, this radius can be derived from equations [ 5 ]:
h = -1109.5aM + 341.67aM – 9.36961aM – 3.9359 (aM < 0.23 pm)
h = 23.909aM -37.218aM +19.534aM – 3.965 (0.23 < aM < 0.60 pm).
These relations are valid for a relative refractive index between equivalent spheres and the surrounding medium equal to m = 1.037.
To describe pulsed light propagation in a tissue, the time-dependent radiation transfer theory is used. This theory is based on the time-dependent linear transport equation, which is a balance equation describing the time-dependent flow of particles (e. g., photons) in a given volume element that takes into account their velocity c, location г, and changes due to collisions (i. e., scattering and absorption).
The time-resolved methods that use pulsed or modulated laser beams for irradiating tissues under study can separate different components of scattering photons from a sample in forward (transillumination) or backscattering operating modes. These groups of photons are so – called ballistic (coherent) photons—a group of unscattered and strictly straightforward scattered photons; quasi-ballistic (snake or zigzag) photons—photons that migrate within a scattering medium along trajectories that are close but not the same as for ballistic photons; and diffusion photons, which are typically the largest group of photons that migrate for a longer time in a tissue along multistep random trajectories. Each of these groups carries information about optical (morphological) properties of a tissue. Ballistic photons are good for getting precise tissue images similar to X-ray computer tomography; however, in many tissues because of strong scattering this group of photons is typically negligibly small. Snake photons, which undergo a few scattering events that are all in the forward or near-forward direction, retain the image bearing characteristics to some extent and are detectable. Due to the high intensity of the diffusion component, it is much more practical to use diffusion photons to estimate optical properties of tissues; however, the spatial resolution may not be very high. To improve the spatial resolution of diffusion methods, various approaches for selective detection of informative photons are suggested, such as spatially-resolved, angle-resolved, and polarization-sensitive gating [1].
One of the parameters which are typically used in tissue study is a scattering spectrum— the spectrum of scattered light; it can be differential, measured or calculated for a certain scattering angle, or integrated within an angle (field of view) of the measuring spectrometer.
The modeling of light propagation in a tissue by taking into account the experimental geometry, source and detector characteristics, and the known optical properties of a sample, and prediction of the measurements and associated accuracies that result are often needed for planning the strategy of light treatment or diagnosis. Such modeling and predictions are classified as a solution of the forward scattering problem. In contrast, the inverse scattering problem solution is the attempt to take a set of measurements and error estimates, and only a limited set of parameters describing the sample and experiment, and to derive the remaining parameters. Usually the geometry is known, intensities or their parameters are measured, and the optical properties or sizes of tissue scatterers need to be derived. If these properties are considered to be spatially varying, then the resultant solutions can be presented as a 2D or 3D function of space, that is, as an image.
All the above-mentioned points are characteristic of elastic (static) light scattering, where light is scattered elastically by static (motionless) objects without changes in photon energy or light frequency. In contrast, the dynamic (quasi-elastic) light scattering involves scattering by a moving object which causes a Doppler shift in the frequency of the scattered wave relative to the frequency of the incident light. A Doppler shift is the apparent change in the frequency of a wave, such as a light wave or sound wave, resulting from a change in the distance between the source of the wave and the receiver.
Inelastic light scattering is a basis for very powerful spectroscopy of biological molecules and tissues, Raman spectroscopy. From quantum theory it follows that an individual light scattering event is considered as an absorption by a particle of the scattering medium of the incident photon with energy h and then emission of the photon with energy hV, at v Ф v" light scattering is accompanied by redistribution of energy between the radiation and the medium and is called inelastic; at v = V scattering is elastic.